2. Construction of twenty elements system on the dodecahedron

 

Before constructing the model using the side chains of amino acids, was built a prototype, the structure of the 20 abstract elements arranged in a dodecahedron. Symbolically elements are denoted by letters of the Latin alphabet and numeric indexes.

 

2.1. Properties of the dodecahedron and the allocation of the planes of antisymmetry in it

 

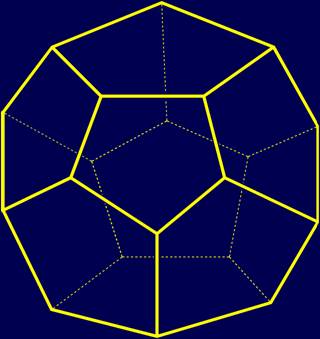
Dodecahedron (Fig. 2) - one of the Platonic bodies. It has 20 vertices, 12 faces and 30 edges.

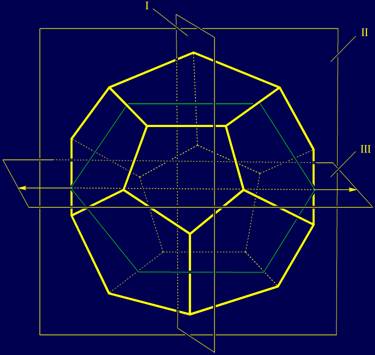
Through dodecahedron vertices it is possible to lead 15 planes.  For our construction, however, we chose three mutually perpendicular planes (Fig. 3), which are not in all "correct" from a mathematical point of view. For our construction it there will be anti-symmetry planes.

 

 

 

 

 

 

 

 

Plane I (quasi-mirror-antisymmetry) is perpendicular to the plane of the sheet and divide the dodecahedron into two equal parts: left and right.

Plane II (not mirror antisymmetry) is in the plane of the sheet and share dodecahedron into two unequal parts:  front and rear.

 

Plane III (rotating antisymmetry) is perpendicular to plane I and horizontal. It shares the dodecahedron into two equal parts - the upper and lower, when rotating around the axis.

Fig. 2. Dodecahedron

 

Рис. 3. Three mutually perpendicular planes, which can be carried through the structure of the dodecahedron.

I - plane of a quasi-mirror antisymmetry;
II - plane of not mirror antisymmetry;
III -  plane of rotary antisymmetry.

 

2.2. Arrangement of elements on a dodecahedron: an antisymmetry principle

 

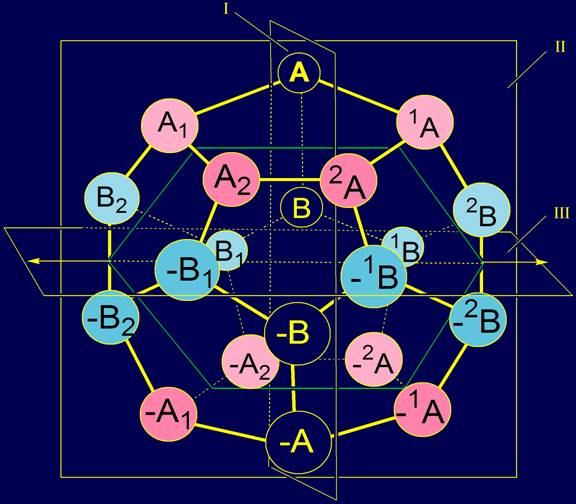
Abstract elements are analogues of the side chains of amino acids. They are  also 20..

 

The first two elements are A and B. Their antipodes are elements –A and –B.

 

The remaining elements were identified on the basis of the letters A and B with indices 1 and 2. For all items that are on the right of the plane I, the indexes are written at the top left of the letters: 1A, 2A,, –1A, –2A and 1B, 2B, –1B, –2B.

 

For elements that are on the left of the plane I the same indices are at the bottom right of the letters: A1, A2, –A1, –A2 and B1, B2, –B1, –B2.

 

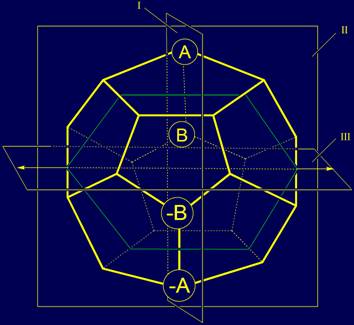
The elements of A, B, and their antipodes –A and –B.
 They have no other antipodes respect to the planes  I and II, so they were placed in the vertices of the dodecahedron, through which plane I passes.  

 

Vertices, where there are elements A and B, and –A, –B, linked by edges.

 

Elements-antipodes are placed symmetrically relative to the plane III, and coincide when rotating around the axis, lying in the plane III: A and -A, B and -B (fig. 4).

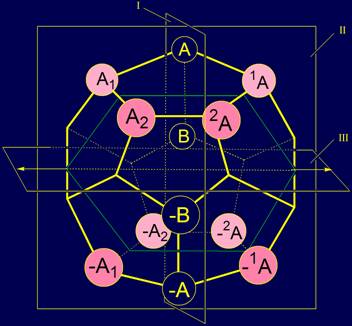
Elements 1A and A1 have been placed in the vertices of the dodecahedron symmetrically to the right and to the left of the plane I and the element  A (Fig. 5), and elements  A2 and A2 are also to the right and to the left, but more far away from the element  A, than the elements A1 and A1.

 

Elements –1A, –A1 and –2A, –A2 will be located in relation to the plane I and the element –A the same way.

 

The arrangement on a dodecahedron of all elements of type A is shown in Figure 5.

Similarly arranged elements of type B.

 

B1 and 1B were located to the right and to the left of the plane I and B element . And the elements B2 and B2 were also placed to the right and to the left, but more far away from the element B, than the previous pair.

 

Elements-antipodes –B1 and  –1B, and –B2  and  –B2 were placed on either side of the plane I and element –B.

 

The arrangement on a dodecahedron of elements of type B is shown in Figure 6.

Fig. 4. Location on the dodecahedron of  elements A, B, -A, -B, which don’t have antipodes respect to the planes  I and II .

Fig. 5. The arrangement on a dodecahedron of symmetric elements of type A.

Fig. 6. The arrangement of elements of type B on a dodecahedron.

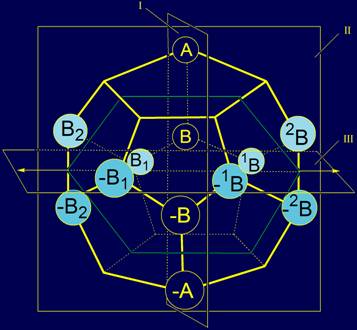
The whole system of 20 elements, located on the dodecahedron is shown in figure 7.

Fig. 7. The system of elements of type A and B on the dodecahedron.

As a result we have received four subgroups of elements: 

Two subgroups of two elements:Subgroup 1: A and –A, a subgroup 2: B and –B;

Two subgroups of 8 elements: Subgroup 3: 1A and A1, 2A and A2, –1A and –A1, –2A and–A2; Subgroup 4: 1B and B1, 2B and B2, –1B and–B1, –2B and –B2.

 

 

2.3. Transformations of elements at transition through antisymmetry planes

 

Since we have three planes of antisymmetry, then the transition through this plane to symmetric element may be designated by any letter.

The following notation were introduced:

- Transition through a plane I - the letter a (alpha),

- Transition through a plane II - the letter b (бета);

- Rotation round an axis laying in a plane III - the letter g (gamma).

 

Then it is possible to describe all transformations of the elements, located in a column 1 in each group, in the form of the following table.

 

 

1

a

b

g

ab

ag

bg

abg

Subgroup 1

А

 

 

- А

 

 

 

 

Subgroup 2

B

 

 

- B

 

 

 

 

Subgroup 3

A1

1A

A2

-A1

2A

-1A

-A2

-2A

Subgroup 4

B1

1B

B2

-B1

2B

-1B

-B2

-2B

 

In the process of further presentation, which is performed in section 3, Twenty side chains of amino acids were divided into four similar subgroups which will be referred to as subgroup 1, subgroup 2, etc.

 

 

To the main page

 

Address for connection: amino-acids-20@yandex.ru 

 

Сайт управляется системой uCoz