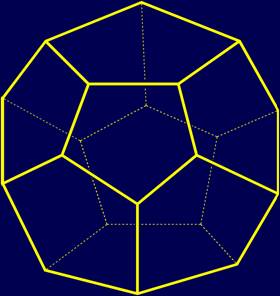
Додекаэдр (рис.2) -  одно из тел Платона. Он содержит 20 вершин, 12 граней и 30 ребер.

Через вершины додекаэдра можно провести 15 плоскостей.

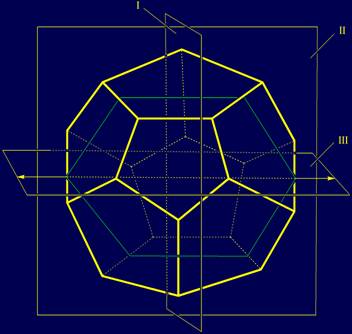
Для нашего построения, однако, были выбраны три взаимно перпендикулярных плоскости (рис.3), которые не во всем являются «правильными» с математической точки зрения. Для нашего построения это будут плоскости анти-симметрии.

Плоскость I  (квази-зеркальной антисимметрии) перпендикулярна плоскости листа и делит додекаэдр на две равные части – правую и левую.

Плоскость II (незеркальной антисимметрии) находится в плоскости листа и разделяет додекаэдр на две неравные части – переднюю и заднюю.

Плоскость III (повортной антисимметрии) перпендикулярна плоскости I и расположена горизонтально.  Она разделяет додекаэдр на две равные части – верхнюю и нижнюю, которые при вращении вокруг оси, лежащей в плоскости III полностью совмещаются друг с другом.

Рис. 2. Додекаэдр

Рис. 3. Три взаимно перпендикулярных плоскости, которые можно провести  через структуру додекаэдра.

I – плокость квази-зеркальной антисимметрии;

II – плоскость незеркальной антисимметрии;

III – плоскость поворотной антисимметрии.

Абстрактные элементы являются аналогами боковых цепей аминокислот. Их  также 20.

Первые 2 элемента: A и B.  Их антиподами являются элементы –A и –B.

Остальные элементы были обозначены на основе букв A и B с помощью индексов 1 и 2. Во всех элементах, которые находятся справа от плоскости I, эти индексы  записаны вверху слева от букв:  ¹A, ²A, , –¹A, –²A и ¹B, ²B, –¹B, –²B. 

В элементах расположенных слева от плоскости I  те же индексы находятся внизу справа от букв: A₁, A₂,  –A₁, –A₂ и B₁, B₂, –B₁, –B₂.

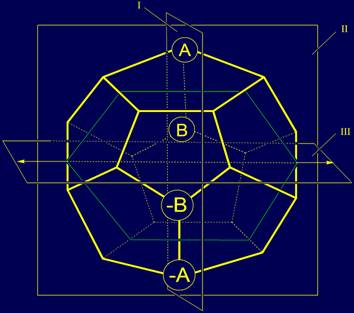
Элементы A, B, и их антиподы –A и –B.

 Они не имеют других антиподов относительно плоскостей I и II, поэтому они были помещены в вершины додекаэдра, через которые проходит плоскость I.

Вершины, где находятся элементы A и B, а также  –A, –B, связаны между собой ребрами.

Элементы-антиподы помещены симметрично относительно плоскости III, и совпадают при вращении относительно оси, лежащей в плоскости III: A и –A, B и –B (рис. 4).

Элементы ¹A и A₁ были помещены в вершины додекаэдра симметрично справа и слева от плоскости I и элемента A (рис.5), а элементы A² и A₂ также справа и слева, но подальше от элемента А, чем элементы A¹ и A₁.

Точно так же по отношению к плоскости I  и элементу –A будут  располагаться элементы   –¹A, –A₁ и –²A, –A₂.

Расположение на додекаэдре всех элементов типа A  показано на рисунке 5.

Аналогичным образом расставляются элементы типа  B.

Справа и слева от плоскости I  и элемента B были расположены B¹ и ₁B, а элементы B² и B₂ также помещены справа и слева, но подальше от элемента B, чем предыдущая пара.

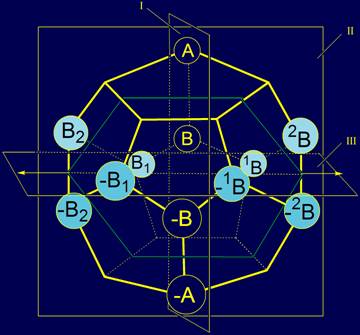
Элементы-антиподы –B¹ и –₁B, а также –B² и –B₂ были помещены справа и слева от плоскости I и элемента –B.

Расположение на додекаэдре элементов типа B показано на рисунке 6.

Рис. 4.  Положение на додекаэдре элементов A, B, –A, –B, не имеющих антиподов относительно плоскостей I и II.

Рис. 5. Расположение на додекаэдре симметричных элементов типа A.

Рис.6. Местонахождение элементов типа B на додекаэдре.

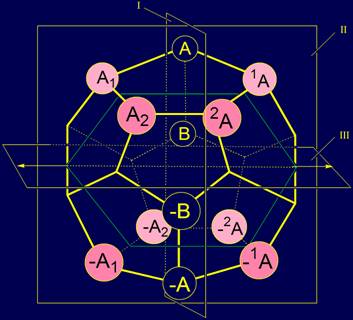
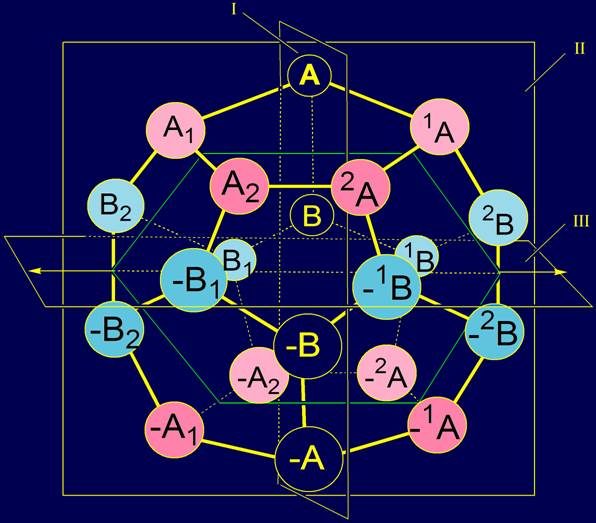
Вся система из 20 элементов, расположенная  на додекаэдре, показана на рисунке 7.

Рис. 7. Система элементов типа A и B на додекаэдре.

В результате мы получили четыре подгруппы элементов.  Две подгруппы по два элемента: подгруппа 1:  A и –A;  подгруппа 2: B и –B;